A concept related to rate of appearance, particularly applicable to the progress in one direction only of component reaction steps in a complex system or to the progress in one direction of reactions in a system at dynamic equilibrium (in which there are no observable concentration changes with time). Chemical flux is a derivative with respect to time, and has the dimensions of amount of substance per unit volume transformed per unit time. The sum of all the chemical fluxes leading to destruction of B is designated the 'total chemical flux out of B' (symbol 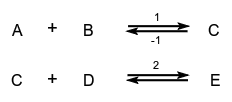$\sum {\phi }_{-\mathrm{B}}$); the corresponding formation of B by concurrent elementary reactions is the 'total chemical flux into B or A' (symbol $\sum {\phi }_{\mathrm{B}}$). For the mechanism: the total chemical flux into C is caused by the single reaction (1): $$\sum {\phi }_{\mathrm{C}}={\phi }_1$$ whereas the chemical flux out of C is a sum over all reactions that remove C: $$\sum {\phi }_{-\mathrm{C}}={\phi }_{-1}+{\phi }_2$$ where ${\phi }_{-1}$ is the 'chemical flux out of C into B (and/or A)' and ${\phi }_2$ is the 'chemical flux out of C into E'. The rate of appearance of C is then given by: $$\frac{\mathrm{d}[\mathrm{C}]}{\mathrm{d}t}=\sum {\phi }_{\mathrm{C}}-\sum {\phi }_{-\mathrm{C}}$$ In this system ${\phi }_1$ (or $\sum {\phi }_{-\mathrm{A}}$) can be regarded as the hypothetical rate of decrease in the concentration of A due to the single (unidirectional) reaction (1) proceeding in the assumed absence of all other reactions. For a non-reversible reaction: $$\mathrm{A}\stackrel{1}{\to }\mathrm{P}$$ $$-\frac{\mathrm{d}[\mathrm{A}]}{\mathrm{d}t}={\phi }_1$$ If two substances A and P are in chemical equilibrium: $$\mathrm{A}\stackrel{-\rightharpoonup }{\leftharpoondown -}\mathrm{P}$$ then: $$\sum {\phi }_{\mathrm{A}}=\sum {\phi }_{-\mathrm{A}}=\sum {\phi }_{\mathrm{P}}=\sum {\phi }_{-\mathrm{P}}$$ and $$-\frac{\mathrm{d}[\mathrm{A}]}{\mathrm{d}t}=\frac{\mathrm{d}[\mathrm{P}]}{\mathrm{d}t}=0$$